Definition of Neural Networks
Neural Networks are function approximations that stack affine transformations followed by non-linear transformations.
1D Input Linear Neural Networks
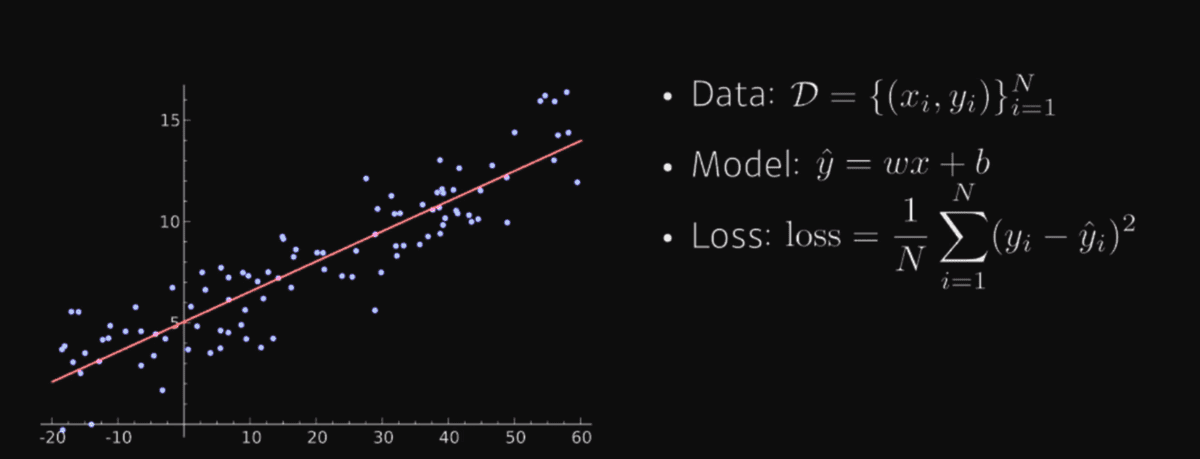
- input is 1d, output is 1d.
- Data is dots on 2d plane
- Model:
y_hat = wx + b - Loss: mean squared error(MSE) as loss function
Minimizing mean squared error loss function based on partial derivative.

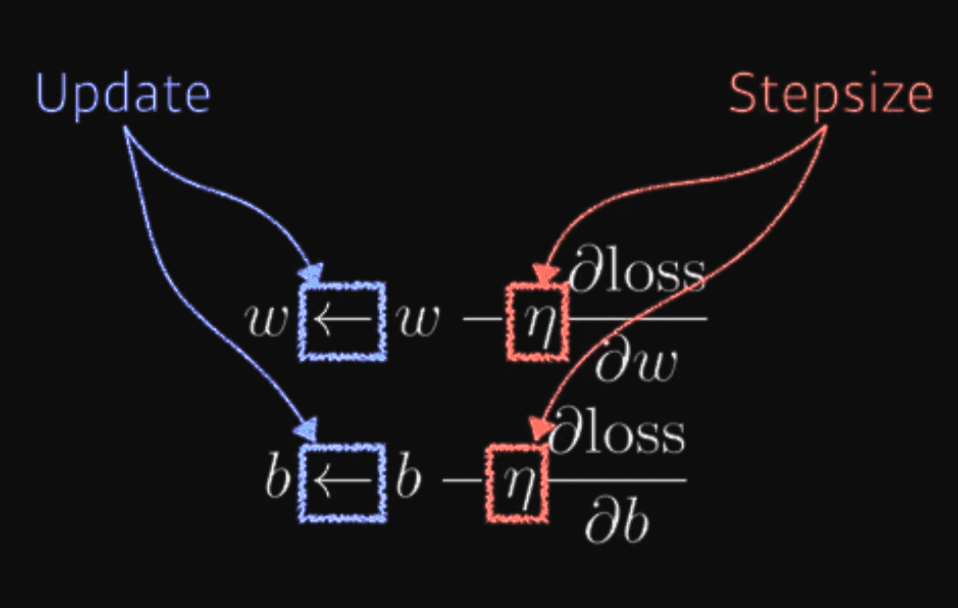
- Backpropagation is (partial) differentiating loss function with all the parameters.
- Gradient descent is the process of updating each individual weights based on partial differentiation value.
- Eta(n) is stepsize.
Multi-Dimensional Input
- Model:
y = W_transpose * x + b

Multi-layer perceptron
Stacking Layers of Matrices and adding non-linear transformation(activation function) in between stacks
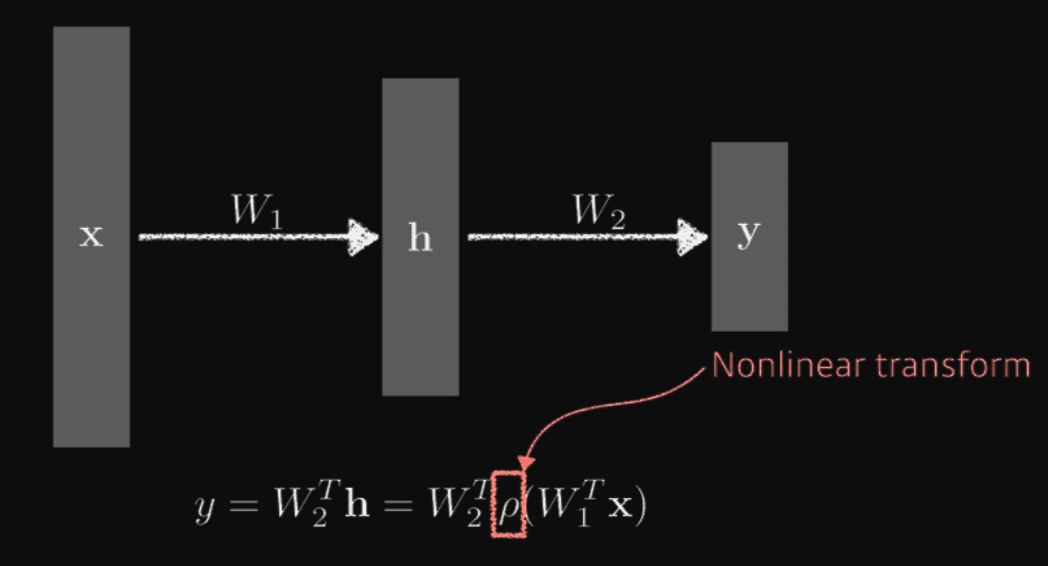
- Model:
W*p*W*x - Universal Approximation Theorem: There is single hidden layer feedforward netowrk that approximates any measurable function to any dessired degree of accuracy on some compact set K.
Loss function

- Regression Task: Mean Squared Error Loss function
- Classification Task: Cross Entropy Loss Function
- Probabilistic Task: