3Blue1Brown Gradient Descent Material
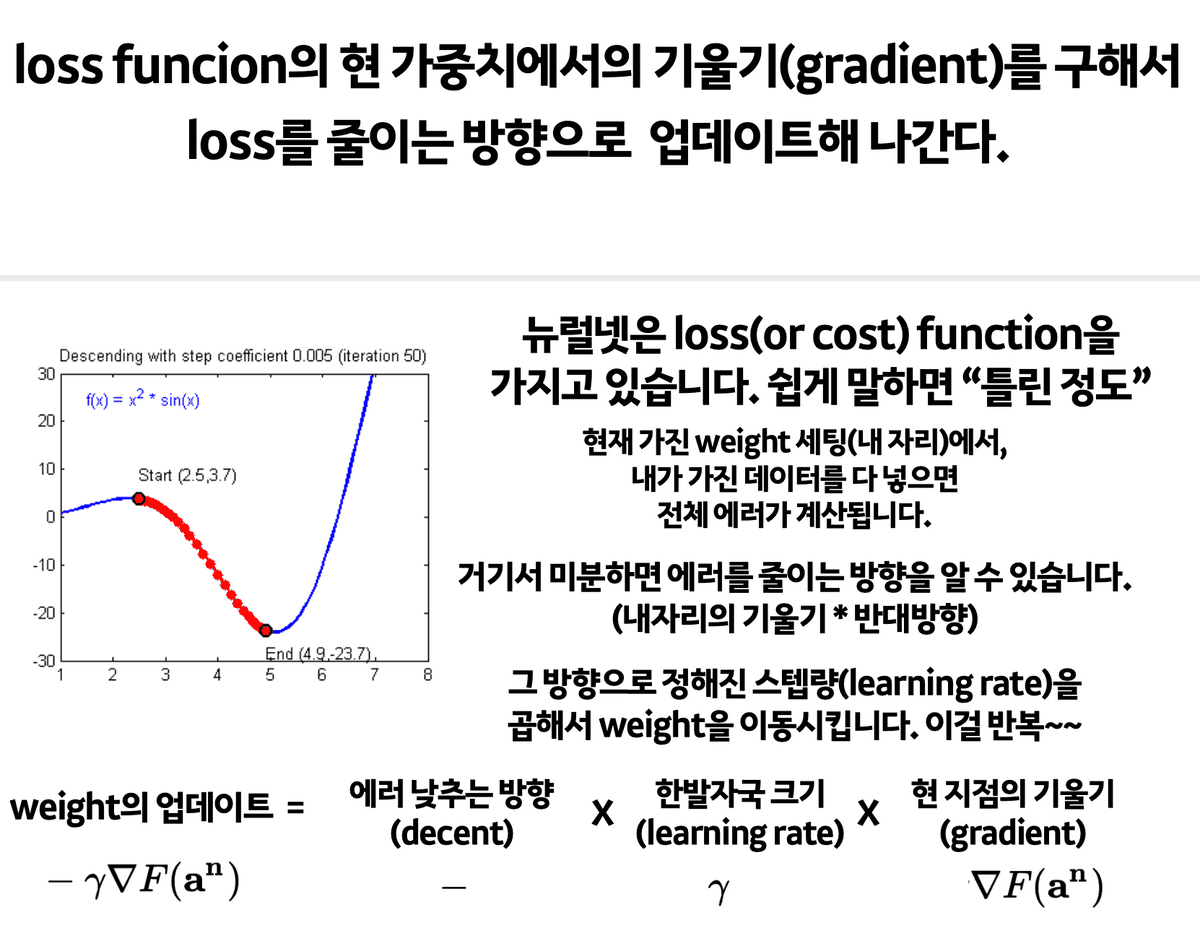
Gradient Descent is 1) first-order 2) iterative optimization algorithm for 3) finding local minimum of a differentiable (loss) function.
"""
This is Gradient Descent using sympy library
"""
import numpy as np
# SymPy is a Python library for symbolic mathematics
# https://www.sympy.org/en/index.html
import sympy as sym
from sympy.abc import x
def make_function_and_value(input_algebraic_notation, input_value):
""" yields both polynomial function and plugin value """
# define polynomial function
polynomial_function = sym.poly(input_algebraic_notation) # x is predefined variable in sympy.abc
# get value by plugging in input_value to x
plugged_in_value = polynomial_function.subs(x, input_value)
# return both the function and the output value
return plugged_in_value, polynomial_function
def yield_gradient_function_and_value(input_function, input_value):
""" yields first-order derivative function(or, gradient function) """
# calculate gradient of input function(or first-order derivative function) using sympy's differential method
gradient_function = sym.diff(input_function, x)
# get the output value by plugin given input_value to x
gradient_value = gradient_function.subs(x, input_value)
# return both the function and the output value
return gradient_value, gradient_function
def gradient_descent(input_function, init_point, lr_rate=1e-2, epsilon=1e-5):
"""
gradient descent algorithm
- init_point: initial point
- lr_rate: learning rate
- epsilon: convergence criteria(think of epsilon and neighborhood)
"""
# initialize variables' default value
iter_cnt = 0 # count of iteration
current_x_val = init_point # current x value
gradient_value, gradient_function = yield_gradient_function_and_value(input_function, current_x_val)
print("Learning rate: {}".format(lr_rate))
print("Initial point: {}".format(current_x_val))
print("Gradient function: {}".format(gradient_function))
print("Convergence criteria: {}".format(epsilon))
# repeat until convergence
while np.abs(gradient_value) > epsilon:
# update current point
current_x_val -= lr_rate * gradient_value
# update gradient of function at current(or moved) point
gradient_value, _ = yield_gradient_function_and_value(input_function, current_x_val)
# show the current point
current_y_val = input_function.subs(x, current_x_val)
# print information on every 10 iterations
if iter_cnt % 10 == 0:
# print current point
print(f"Current point: ({current_x_val}, {current_y_val})")
# print iteration and gradient value(or weight delta)
print("Iteration: {}".format(iter_cnt))
print("Gradient value: {}".format(gradient_value))
# update count of iteration
iter_cnt += 1
# return current point
return [current_x_val, current_y_val]from sympy.abc import x
# get random initial x value
x_starting_pt = np.random.randint(1, 10)
# define polynomial function
_, polynomial_function = make_function_and_value(x**2 + 2*x + 3, x_starting_pt)
gradient_descent(input_function = polynomial_function, init_point = x_starting_pt)Learning rate: 0.01
Initial point: 3
Gradient function: Poly(2*x + 2, x, domain='ZZ')
Convergence criteria: 1e-05
Current point: (2.92000000000000, 17.3664000000000)
Iteration: 0
Gradient value: 7.84000000000000
Current point: (2.20292540299918, 12.2587311371775)
Iteration: 10
Gradient value: 6.40585080599837
Current point: (1.61702324927997, 8.84881068727189)
Iteration: 20
Gradient value: 5.23404649855994
Current point: (1.13829853197915, 6.57232061186421)
Iteration: 30
Gradient value: 4.27659706395831
Current point: (0.747145583487728, 5.05251768990067)
Iteration: 40
Gradient value: 3.49429116697546
Current point: (0.427545145941499, 4.03788514370114)
Iteration: 50
Gradient value: 2.85509029188300
Current point: (0.166408319353113, 3.36050836745615)
Iteration: 60
Gradient value: 2.33281663870623
Current point: (-0.0469594805291656, 2.90828623175324)
Iteration: 70
Gradient value: 1.90608103894167
Current point: (-0.221296507678400, 2.60637912895386)
Iteration: 80
Gradient value: 1.55740698464320
Current point: (-0.363742551795655, 2.40482354039551)
Iteration: 90
Gradient value: 1.27251489640869
Current point: (-0.480131340892568, 2.27026342272216)
Iteration: 100
Gradient value: 1.03973731821486
Current point: (-0.575229455490225, 2.18043001548313)
Iteration: 110
Gradient value: 0.849541089019550
Current point: (-0.652931538914246, 2.12045651668043)
Iteration: 120
Gradient value: 0.694136922171507
Current point: (-0.716419798318522, 2.08041773078571)
Iteration: 130
Gradient value: 0.567160403362956
Current point: (-0.768294328634378, 2.05368751814299)
Iteration: 140
Gradient value: 0.463411342731244
Current point: (-0.810679596725528, 2.03584221509601)
Iteration: 150
Gradient value: 0.378640806548945
Current point: (-0.845311446695445, 2.02392854852346)
Iteration: 160
Gradient value: 0.309377106609111
Current point: (-0.873608189558073, 2.01597488974679)
Iteration: 170
Gradient value: 0.252783620883854
Current point: (-0.896728688674616, 2.01066496374286)
Iteration: 180
Gradient value: 0.206542622650768
Current point: (-0.915619819784411, 2.00712001481322)
Iteration: 190
Gradient value: 0.168760360431179
Current point: (-0.931055249305571, 2.00475337864832)
Iteration: 200
Gradient value: 0.137889501388858
Current point: (-0.943667119029941, 2.00317339347839)
Iteration: 210
Gradient value: 0.112665761940119
Current point: (-0.953971934825732, 2.00211858278369)
Iteration: 220
Gradient value: 0.0920561303485365
Current point: (-0.962391719592458, 2.00141438275521)
Iteration: 230
Gradient value: 0.0752165608150845
Current point: (-0.969271296765196, 2.00094425320249)
Iteration: 240
Gradient value: 0.0614574064696090
Current point: (-0.974892412195924, 2.00063039096534)
Iteration: 250
Gradient value: 0.0502151756081526
Current point: (-0.979485272758748, 2.00042085403378)
Iteration: 260
Gradient value: 0.0410294544825043
Current point: (-0.983237974230458, 2.00028096550790)
Iteration: 270
Gradient value: 0.0335240515390847
Current point: (-0.986304204555359, 2.00018757481286)
Iteration: 280
Gradient value: 0.0273915908892828
Current point: (-0.988809537973489, 2.00012522644037)
Iteration: 290
Gradient value: 0.0223809240530217
Current point: (-0.990856577781630, 2.00008360216986)
Iteration: 300
Gradient value: 0.0182868444367394
Current point: (-0.992529158343479, 2.00005581347506)
Iteration: 310
Gradient value: 0.0149416833130425
Current point: (-0.993895778437894, 2.00003726152088)
Iteration: 320
Gradient value: 0.0122084431242127
Current point: (-0.995012406554386, 2.00002487608838)
Iteration: 330
Gradient value: 0.00997518689122723
Current point: (-0.995924773023779, 2.00001660747491)
Iteration: 340
Gradient value: 0.00815045395244285
Current point: (-0.996670242855835, 2.00001108728264)
Iteration: 350
Gradient value: 0.00665951428833012
Current point: (-0.997279345983963, 2.00000740195827)
Iteration: 360
Gradient value: 0.00544130803207366
Current point: (-0.997777027586547, 2.00000494160635)
Iteration: 370
Gradient value: 0.00444594482690586
Current point: (-0.998183669690506, 2.00000329905579)
Iteration: 380
Gradient value: 0.00363266061898715
Current point: (-0.998515925895787, 2.00000220247595)
Iteration: 390
Gradient value: 0.00296814820842539
Current point: (-0.998787403406042, 2.00000147039050)
Iteration: 400
Gradient value: 0.00242519318791623
Current point: (-0.999009220297352, 2.00000098164442)
Iteration: 410
Gradient value: 0.00198155940529543
Current point: (-0.999190460847351, 2.00000065535364)
Iteration: 420
Gradient value: 0.00161907830529895
Current point: (-0.999338547572259, 2.00000043751931)
Iteration: 430
Gradient value: 0.00132290485548103
Current point: (-0.999459545208244, 2.00000029209138)
Iteration: 440
Gradient value: 0.00108090958351292
Current point: (-0.999558409086304, 2.00000019500254)
Iteration: 450
Gradient value: 0.000883181827392221
Current point: (-0.999639188072650, 2.00000013018525)
Iteration: 460
Gradient value: 0.000721623854699427
Current point: (-0.999705190385762, 2.00000008691271)
Iteration: 470
Gradient value: 0.000589619228476224
Current point: (-0.999759119080997, 2.00000005802362)
Iteration: 480
Gradient value: 0.000481761838005967
Current point: (-0.999803182751385, 2.00000003873703)
Iteration: 490
Gradient value: 0.000393634497230400
Current point: (-0.999839185978230, 2.00000002586115)
Iteration: 500
Gradient value: 0.000321628043539857
Current point: (-0.999868603235846, 2.00000001726511)
Iteration: 510
Gradient value: 0.000262793528308602
Current point: (-0.999892639277096, 2.00000001152632)
Iteration: 520
Gradient value: 0.000214721445807253
Current point: (-0.999912278472788, 2.00000000769507)
Iteration: 530
Gradient value: 0.000175443054424296
Current point: (-0.999928325125536, 2.00000000513729)
Iteration: 540
Gradient value: 0.000143349748927157
Current point: (-0.999941436409139, 2.00000000342969)
Iteration: 550
Gradient value: 0.000117127181722188
Current point: (-0.999952149282434, 2.00000000228969)
Iteration: 560
Gradient value: 0.0000957014351326002
Current point: (-0.999960902479887, 2.00000000152862)
Iteration: 570
Gradient value: 0.0000781950402268805
Current point: (-0.999968054479499, 2.00000000102052)
Iteration: 580
Gradient value: 0.0000638910410024618
Current point: (-0.999973898183897, 2.00000000068130)
Iteration: 590
Gradient value: 0.0000522036322065933
Current point: (-0.999978672915852, 2.00000000045484)
Iteration: 600
Gradient value: 0.0000426541682967407
Current point: (-0.999982574219492, 2.00000000030366)
Iteration: 610
Gradient value: 0.0000348515610157918
Current point: (-0.999985761868608, 2.00000000020272)
Iteration: 620
Gradient value: 0.0000284762627837942
Current point: (-0.999988366410019, 2.00000000013534)
Iteration: 630
Gradient value: 0.0000232671799620388
Current point: (-0.999990494509980, 2.00000000009035)
Iteration: 640
Gradient value: 0.0000190109800397575
Current point: (-0.999992233322589, 2.00000000006032)
Iteration: 650
Gradient value: 0.0000155333548226277
Current point: (-0.999993654059087, 2.00000000004027)
Iteration: 660
Gradient value: 0.0000126918818252886
Current point: (-0.999994814904246, 2.00000000002689)
Iteration: 670
Gradient value: 0.0000103701915079579
[-0.999995020234038, 2.00000000002480]